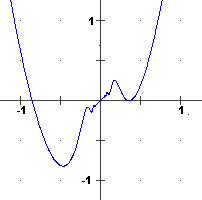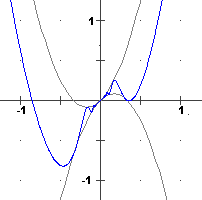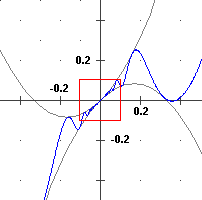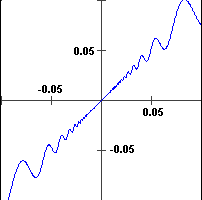
Sia F così definita:             F(x) = x + 3x2·cos(1/x)   se x ≠ 0             F(0) = 0. Si tratta di una funzione derivabile anche in 0, con  F'(0) = 1 > 0: il suo grafico oscilla tra le curve  y = x + 3x2  e  y = x - 3x2  e  per x → 0  tende a spiaccicarsi sulla retta  y = x  tangente ad esse. Ma è una funzione che non è crescente in alcun intervallo contenente 0. Infatti  per x → 0  oscilla con frequenza tendente all'infinito:  comunque mi avvicini a 0 trovo sia dei tratti in cui il grafico sale che dei tratti in cui scende  (passando dal punto in cui tocca una delle due parabole a quello in cui tocca l'altra deve, alternatamente, passare da una situazione di crescita a una di decrescita e viceversa). È un caso in cui la funzione derivata  F'  è definita in (-∞, ∞) ma è continua solo in (-∞, 0) e in (0, ∞).